After my summer conference travels, I felt even more desolate. Since Eric had returned to Berkeley, I was able to go for weeks without anyone knowing or caring how I was spending my time. My sleep schedule quickly turned upside-down, and I found myself compulsively scrolling Facebook for hours at a time — which I now recognize as a mechanism for attempting to avoid my fear of failure.
At the times when I did manage to get myself to work, I’d throw myself headlong into Matt’s idea of transchromatic detection. I envisioned this as my moment of truth: the moment when I would need to work incredibly hard, if I wanted to have any chance at being truly good at math. But rather than feeling joy or excitement as I engaged with this gorgeous idea, I felt dread — precisely commensurate with the intensity of my self-expectations. On the shiny spaceship of TMF, where could I even begin to sink my hooks? The entire endeavor felt doomed from the outset.
Attempting to move forward with transchromatic detection became increasingly painful, and I began to find solace in turning backward. I figured that I could only really understand TMF — and thereafter, do something with it — if I understood exactly how it was constructed: whereas most people treated the construction of TMF as a black box, I set about opening up the box.12 The construction of TMF — or at least, the only construction known at the time — rests on an extremely complex and intricate tool called Goerss—Hopkins obstruction theory, which I began referring to as GHOsT for short.3 So, I set about working to understand GHOsT.
Diving into GHOsT gave me a deep sense of peace and safety. It was so sprawling that I could reaaaaally sink my teeth into it, nevertheless feeling as purposeful as ever in moving towards my goal of doing something with TMF.
However, as the totality of GHOsT slowly hove into view in my mind’s eye, I was surprised to find that I actually felt wisps of fear. Concluding my engagement with GHOsT would mean that it would be time for me to return to TMF, and therefore to face my moment of truth once more.
As it turned out, such a conclusion never materialized.
I was invited to give a lecture in late November over in Regensburg, another German homotopy theory hotspot. I spoke there about my vague but captivating ideas around transchromatic detection in TMF — ideas I’d inherited from Matt, obviously, which were not really any closer to being realized than when he’d first shared them with me.
I stayed in Regensburg for a few days after the lecture so that I could continue meeting with my host, Niko. Our meetings left me with a tentative sense of hope: he shared some helpful thoughts on transchromatic detection, and suggested another project that I might pursue as well. (Maybe that project would be the one to save me??!?) But the interaction that truly shaped my future almost didn’t happen.
Markus was another German homotopy theorist who happened to be visiting Regensburg at the same time. Since he was based in Osnabrück, he’d be passing near Bonn on his way home, and so we happily agreed to share the train ride.
Markus worked in the area of motivic homotopy theory,4 and shared his dream of constructing of a motivic version of TMF:5 a dream that he’d happily transfer over to me, and support me in bringing to fruition — starting with introducing me to the basics of the motivic world as we rode the train home together.
Wait a second. Could this be it?! I had spent so much time and energy understanding GHOsT, the essential tool for constructing TMF. And so the challenge effortlessly offered itself to my imagination: to construct a motivic version of GHOsT. And thereby, to become.
This is a painfully transparent instance of the typical behavior of a “Type Five” in the Enneagram personality typography, which describes me eerily well and which I believe applies to a majority (or at least a plurality) of mathematicians more broadly. In the face of fear or uncertainty, we Fives tend to over-conceptualize and over-prepare, assiduously gathering resources and conducting deeper and deeper background investigations as a (generally subconscious) means of avoiding actual action. It feels safer.
Early in one’s math career (e.g. as an undergrad), one is generally advised to make sure that one understands absolutely everything from the ground up. The proof of Theorem A is based upon Propositions B and C, which in turn follow from Lemmas D and E, all of which rests on Axiom Z: one verifies everything for oneself, taking nothing for granted. (Along these lines, I appreciate the assertion that the fundamental transferrable skill of a mathematician is knowing what it is to fully understand — and thus also and equivalently knowing what it is to not fully understand (assuming the law of the excluded middle). (This assertion harmonizes beautifully with the ideas put forth in Bill Thurston’s eye-opening essay On Proof and Progress in Mathematics.))
By contrast, as one matures mathematically, one may come to appreciate the importance of “black-boxing” certain pieces of one’s mathematical landscape. The utility of this practice is well explained by the following advice to students from Ravi Vakil (with extra spacing added for readability).
Here’s a phenomenon I was surprised to find: you’ll go to talks, and hear various words, whose definitions you’re not so sure about. At some point you’ll be able to make a sentence using those words; you won’t know what the words mean, but you’ll know the sentence is correct. You’ll also be able to ask a question using those words. You still won’t know what the words mean, but you’ll know the question is interesting, and you’ll want to know the answer. Then later on, you’ll learn what the words mean more precisely, and your sense of how they fit together will make that learning much easier.
The reason for this phenomenon is that mathematics is so rich and infinite that it is impossible to learn it systematically, and if you wait to master one topic before moving on to the next, you’ll never get anywhere. Instead, you’ll have tendrils of knowledge extending far from your comfort zone. Then you can later backfill from these tendrils, and extend your comfort zone; this is much easier to do than learning “forwards”.
(Caution: this backfilling is necessary. There can be a temptation to learn lots of fancy words and to use them in fancy sentences without being able to say precisely what you mean. You should feel free to do that, but you should always feel a pang of guilt when you do.)
Of course, one of the wonderful and profoundly satisfying features of mathematics is that the details are (essentially) always available, and one is utterly free to open and explore whichever black boxes one wishes. And as always, the decisions that we make determine who we become. (Among many other effects, these decisions of which black boxes to open bear upon a mathematician’s identity along the spectrum between “bird” and “frog” in the sense of Freeman Dyson’s lovely Birds and Frogs lecture.)
Although establishing GHOsT was an extremely difficult task (which Goerss and Hopkins — two luminaries in the field — accomplished iteratively over the course of seven papers totaling around 400 pages), using it is a deceptively simple and elegant matter: GHOsT defines a big list of numbers, and if one manages to compute them and finds that they are all zero, then TMF must exist!
Specifically, these numbers quantify the totality of all possible “obstructions” to the existence of TMF. This beautifully illustrates the nature of the construction of mathematical objects in general, which arises not through physical effort like the construction of a bridge or freeway but rather through a profound form of necessity. In the present situation, once it was proved that these obstructions all vanish, it was as if the mathematical universe — finding every possible objection silenced — had no choice but to yield to TMF its place in the family of things.
Motivic homotopy theory extends the world of ordinary homotopy theory, so that it can be applied in the context of algebraic geometry. The development of modern algebraic geometry is far too beautiful not to include at least a brief hint of it here.
Interestingly, a motivic version of TMF would have two separate (and orthogonal, at least a priori) connections to number theory: one through its motivic nature (which connects it to algebraic geometry) and one through its connection to TMF itself (which is a topological enhancement of modular forms, which come directly from number theory).


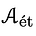

Hi Aaron, I'm an avid reader of your blog, and I was a bit sad to not find an update last week (and this week). I hope everything is okay on your end. Could you please keep us posted. Love.