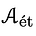"On Life and Math", Chapter 4: Bonn Hiver (Part 2 of 3)
That summer found me on a whirlwind 2.5-month tour of math conferences around Europe — traveling (from Bonn, natürlich) to Austria, France, Denmark, Germany (elsewhere), and Switzerland. Driven by my desire to work on TMF, I found myself “interviewing” TMF experts whenever I met them. They freely shared vague but captivating intimations about TMF and its further connections to number theory, which involved such sexy-sounding concepts as Dieudonné crystals and overconvergent p-adic modular forms. I distinctly remember the feeling of hunting for all-but-impossible table scraps: strategies for turning these intimations into actual theorems that were simultaneously easy enough that I could pursue them on my own but hard enough that these experts had somehow missed them themselves.
Among the various ideas about TMF that I acquired during my interviews, I felt particularly hopeful by one regarding transchromatic detection, which had been magnanimously gifted to me by Matt, Eric’s research supervisor during his post-undergrad gap year. TMF encompasses “chromatic heights” 0, 1, and 2, but the height-2 parts of it manifest as isolated peaks surrounded entirely by height-1 terrain. So, drawing inspiration from number theory, the idea was to find a way of detecting the height-2 peaks while observing just the height-1 terrain — the way rings of clouds might allude to the existence of a mountain peak even as they obscure the peak itself (see below).1

Despite my gratitude for these interviews, on a mostly-unconscious level I was very much aware of the unlikelihood of such table scraps. That caused me deep-seated feelings of disempowerment and hopelessness, especially given my commitment to myself that I’d manage to do something with TMF — a commitment which had mutated from a dreamy possibility into a daunting and inescapable challenge.
Exacerbating these feelings, Eric had had a research breakthrough just a few months earlier. When he first told me about it, I felt joy for his success, awe at the beauty of his ideas, but most of all envy for him having discovered the ideas that would become his PhD thesis. I remember trying my best to ask him probing questions, with the painfully unrealistic hope that I would uncover something — either a gap in his ideas or an extension of them — so that he would feel compelled to invite me to join him as a collaborator. I felt a fear of being left behind… of never truly becoming.
In the world of number theory, the clouds in this analogy correspond to p-adic modular forms for height-1 (a.k.a. ordinary) framed elliptic curves. These give a nontrivial covering space of the height-1 locus (the terrain below the ring of clouds), which is in fact maximally nontrivial in the sense that over a punctured neighborhood of each height-2 (a.k.a. supersingular) point it is recorded by a surjection from the étale fundamental group onto the associated automorphism group — a phenomenon discovered by Jun-ichi Igusa and explained beautifully by Nick Katz in p-adic Properties of Modular Schemes and Modular Forms (his so-called “Antwerp Notes”).